haya14busa

haya14busa’s memo

数学ガールフェルマーの最終定理読んだメモ

- -

Web連載『数学ガールの秘密ノート』

プロローグ

「整数は神の作ったものだが、他は人間の作ったものである」(Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk.)

– レオポルト・クロネッカー – Wikipedia

無限の宇宙を手に乗せて

時計の巡回

「ではみなさんは、そういうふうに川だと云われたり、乳の流れたあとだと云われたりしていたこのぼんやりと白いものがほんとうは何かご承知ですか。」

– 宮沢賢治 銀河鉄道の夜

ピタゴラスの定理

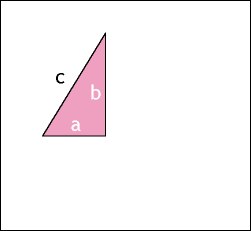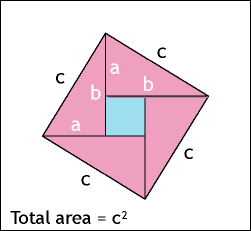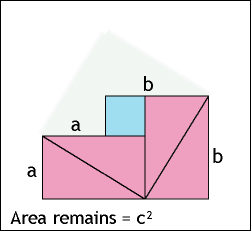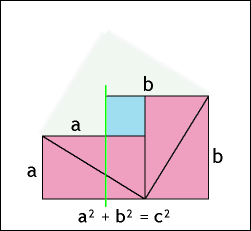
pytagorean_proof_by_gif

Card: Tetra

  1. <<例示は理解の試金石>>
    • 具体的に探してみる
  2. 偶奇を調べる(パリティチェック)
    1. a,bが偶数の原始ピタゴラス数は存在するか
    2. a,bが奇数は？
    3. c2は4の倍数
    4. 背理法
  3. <<和の形>>から<<積の形>>へ
    1.  <<整数の構造は、素因数が示す>>
    2. b2 = (c-a)(c+a)とa,b,cの偶奇を組み合わせる
  4. 互いに素
    1. <<わかりきっていることでも、きちんとまとめるのがいいんだよ>>
    2. a,c,b、A,B,Cについて互いに素であるか？
    3. aを奇数として
    4. 2A = c – a
    5. 2B = b
    6. 2C = c + a
    7. Pattern: 互いに素の証明は、背理法で同じ倍数になるという矛盾を導く
  5. 素因数分解
    • 素因数分解の一意性 -> A,Cは平方数

  6. 原子ピタゴラス数の一般形

    • 無数にある素数から無数の原子ピタゴラス数を作り上げる

  7. <<偶奇を調べる>>

  8. <<整数の構造は、素因数が示す>>
  9. <<積の形>>
  10. <<互いに素>>

Card: Milka

  1. <<有理点が無数にある>>という命題は、方程式x^2 + y^2 = 1が<<無数の有理数解を持つ>>という命題と同値
  2. P(-1,0)を通り、傾きがtの直線l: y = tx + tと単位円x^2+y^2=1のもう一つの交点Qをtで表す
  3. 点Tがy軸上の有理点ならば、点Qも有理点になる

原始ピタゴラス数の問題との関連

ピタゴラスの定理を変形

a^2 + b^2 = c^2
(a/c)^2 + (b/c)^2 = 1 -> 単位円

<<有理数の構造は、整数の比が示す>>

<<原始ピタゴラス数が無数にある>>と<<単位円周上に有理点が無数にある>>は同値

Link

互いに素

自然数a,bの最大公約数をM、最小公倍数をLで表すと、このとき

a \* b = M \* L

が成り立つ

  • a * b : <<aの素因数すべて>>と<<\bの素因数すべて>>
  • M * L :   – M : <<aとbでだぶっている素因数すべて>>   – L : <<aとbでだぶりを除いた素因数すべて>>

素数指数表現

n = 2^n_2 \* 3^n_3 \* 5^n_5 ....
  = <n_2, n_3, n_5, ....>
  • 無限次元のベクトルとみなして考えることができる
    • 互いに素のとき、ベクトルが直交する
  • mとnが互いに素のとき m⊥nと表す

背理法

矛盾
Pを命題とする。 矛盾とは、<<\Pである>>と<<\Pでない>>の両方が成り立つこと

√2が有理数でないことを、背理法以外に素因数の個数のパリティで証明できる

<<素因数分解の一意性により、素因数の個数は、素因数ごとに両辺で一致する>>

砕ける素数

1次元から2次元への飛躍

<<二乗して-1になる数>>を幾何の目で見るなら、
二回行うと-1になる拡大・回転は何か?

(-1) * (-1) = 1は-1の偏角180度を二倍することに相当する -> 360度の回転

回れ右を二回行えば元の向きに戻る

代数 <-> 幾何 複素数全体の集合 <-> 複素平面 複素数a+bi <-> 複素平面上の点(a,b) 複素数の集合 <-> 複素平面上の図形 複素数の数 <-> 平行四辺形の対角線 複素数の積 <-> 絶対値の積、偏角の和(拡大・回転)

格子点

鳩の巣原理
n個の鳩ノ巣にn+1羽の鳩が入ったら、
少なくとも1個の巣には、2羽の鳩がいる。
ただし、nは自然数とする。

砕ける素数

砕ける素数を4で割った余りは3にならない。

p = (a + bi)(a - bi)

pを奇数の素数にすると、

p = (a + bi)(a - bi) <-> pを4で割ると余りは1

アーベル郡の涙

素数 (Prime number)の全体、射影空間など

自然数 (Natural number)の全体

整数 (独: Zahlen)の全体

有理数 (Quotient)の全体

実数 (Real number)の全体

複素数 (Complex number)の全体

四元数 (Hamilton number)の全体

– 数学記号の表 – Wikipedia

集合に対して演算を入れる

集合Gに対して、演算☆が定義されるとは、集合Gのどんな要素a,bに対しても、

a ☆ b ∈ G

が成り立つということ。これを<<演算☆に関して集合Gは閉じている>>と呼ぶ

  • a ∈ G
    • aはGの要素である
    • a is an element of G
    • a belongs to G
    • a is in G
  • G -> Group

結合法則

(a ☆ b) ☆ c = a ☆ (b ☆ c)
単位元の定義(単位元eの公理)

集合Gの任意の要素aに対して、以下の式を満たす集合Gの要素eを、演算☆における単位元と呼ぶ。

a ☆ e = e ☆ a = a

<<公理が定義を生み出している>>
最も厳密な言葉である数式を使い、公理という名の命題を使って定義する
逆元の定義(逆元の公理)
aを集合Gの要素とし、eを単位元とする。aに対して、以下の式を満たすb∈Gを、演算☆に関するaの逆元と呼ぶ。 ~~~ a ☆ b = b ☆ a = e ~~~

郡の定義(郡の公理)

以下の公理を満たす集合Gを郡と呼ぶ。

  • 演算☆に関して閉じている
  • 任意の元に対して、結合法則が成り立つ。
  • 単位元が存在する。
  • 任意の元に対して、その元に対する逆元が存在する。

かくのごとき集合を郡と呼べ

<<例示は理解の試金石>>

  • <<整数全体の集合Ζは、演算+に関して郡をなすか?>>
  • <<奇数全体の集合Ζは、演算+に関して郡をなすか?>>
  • <<偶数全体の集合Ζは、演算+に関して郡をなすか?>>
  • <<整数全体の集合Ζは、演算×に関して郡をなすか?>>

例

  • 最小の郡
    • {e}
  • 要素が2個の群
    • {e,a}

演算表

|☆ | e a|
|---+----|
|e  | e a|
|a  | a e|
  • <<同じ>>郡のことを<<同型>>な郡と呼ぶ
  • <<要素が二つの郡は本質的に一つ>>
    • 公理によって与えられる制約が構造を生み出している

アーベル群

交換法則

a ☆ b = b ☆ a

<<無矛盾性は存在の礎>>

ヘアスタイルを法として

modの定義(整数)

a,b,q,rは整数で、b≠0とする

a mod b = r ⇔ a = bq + r (0 ≤r < |b|)

合同(congruent modulo)

a ≡ b (mod m) ⇔ a mod m = b mod m ⇔ (a-b) mod m = 0

郡・環・体

環の定義(環の公理)
以下の公理を満たす集合を環とよぶ
  • 演算+(加法)に関して
    • 閉じている
    • 単位元が存在する(0と呼ぶ)
    • すべての要素について結合法則が成り立つ
    • すべての要素について交換法則が成り立つ
    • すべての要素について逆元が存在する
  • 演算×(乗法)に関して
    • 閉じている
    • 単位元が存在する(1と呼ぶ)
    • すべての要素について結合法則が成り立つ
    • すべての要素について交換法則が成り立つ
  • 演算+と×に関して
    • すべての要素について分配法則が成り立つ

厳密に言えば乗法の単位元が存在する可換環を述べている

  • 環と郡
    • 環は、加法に関してアーベル群である。
    • 環は、乗法に関してアーベル郡とは限らない。

整数環と剰余環

体の定義(体の公理)
環の定義プラス、演算×に関して0以外のすべての要素について逆元が存在する

剰余環Ζ/mΖは、mが素数のとき体になる

pを素数とし、剰余環Ζ/mΖを体と見なすとき、それを有限体F_pと呼ぶ

F_p = Ζ/pΖ

合同を使って<<無限を折りたたむ>>

無限降下法

次の方程式は、n ≥3で自然数解を持たない。

x^n + y^n = z^n

私は驚くべき証明を見つけたが、
それを書き記すには、この余白は狭すぎる。

FLT -> Fermat’s Last Theorem

Card: Tetra

三辺が自然数で面積が平方数である直角三角形は存在するか。

無限降下法
  1. 自然数に関する数式を作る。
  2. その数式を操作して、同じ形をした別の数式を作る
    • このとき、小さくなる自然数を含む
  3. 同じ操作を繰り返すと自然数が無限に小さくなる -> 矛盾

Card: Milka

FLT(4)の証明

Card: Tetraの解答を使って矛盾を示す

最も美しい数式

Euler’s identity

e^iπ = -1

Euler’s formula

e^iθ = cosθ + isinθ

最も美しい数式

“Is the term ‘well-defines’ well defined?”

  1. 指数を指数法則を満たすものと定義
    • 自然数以外への拡張
  2. exを冪級数で表す
  3. テイラー展開
  4. テイラー展開の結果をexと定義
    • 複素数への拡張
  5. eiθを<<大胆な代入>>
  6. cosθとsinθのテイラー展開の結果と比較する

フェルマーの最終定理

Comments